Notice
Recent Posts
Recent Comments
Link
| 일 | 월 | 화 | 수 | 목 | 금 | 토 |
|---|---|---|---|---|---|---|
| 1 | 2 | 3 | 4 | 5 | ||
| 6 | 7 | 8 | 9 | 10 | 11 | 12 |
| 13 | 14 | 15 | 16 | 17 | 18 | 19 |
| 20 | 21 | 22 | 23 | 24 | 25 | 26 |
| 27 | 28 | 29 | 30 | 31 |
Tags
- Bubble Sort
- 공채
- sorting
- Subset
- 스택
- stack
- Linked List
- Medium
- Easy
- 트리
- 배열
- 완전검색
- list
- bst
- Bit
- 순회
- leetcode
- tree
- 오픈 채팅방
- binary search tree
- 카카오
- Math
- kakao
- 2019 카카오
- 리스트
- 정렬
- LinkedList
- traversal
Archives
- Today
- Total
미리수얌 블로그
Bubble Sort (버블 정렬) 본문
Bubble Sort
버블 정렬은 두개의 숫자를 버블로 묶어서 뒤에 있는 숫자가 작을 때
바꾸어 주는 정렬입니다.
예를 들어 [2, 7, 3, 1, 6] 이라는 배열이 주어줬을때
첫번째 돌아갔을때
- [2, 7, 3, 1, 6] => (2, 7) 7이 더 큼 no swap
- [2, 7, 3, 1, 6] => (7, 3) 3이 더 작음 swap -> [2, 3, 7, 1, 6]
- [2, 3, 7, 1, 6] => (7, 1) 1이 더 작음 swap -> [2, 3, 1, 7, 6]
- [2, 3, 1, 7, 6] => (7, 6) 6이 더 작음 swap -> [2, 3, 1, 6, 7]
한번 돌아 갔을때 보면 가장 큰 수가 맨 오른쪽으로 이동 하는것을 볼 수 있습니다.
이것을 정렬이 될 되 까지 하면 됩니다.
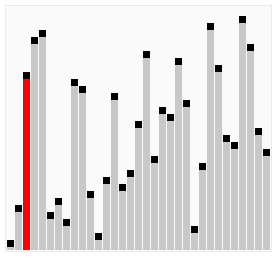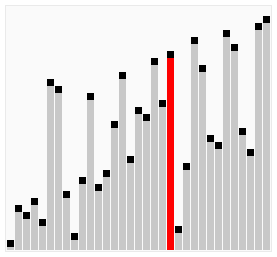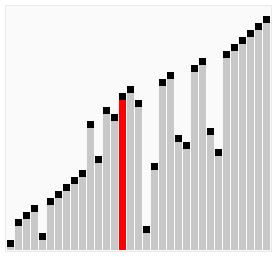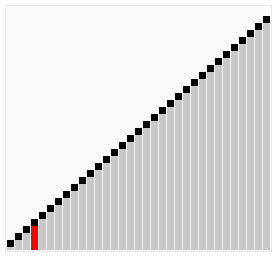
출처: wikimedia
이 영상을 보면 좀더 이해가 가실 겁니다.
swap 코드
private void swap(int[] arr, int i, int j) {
int tmp = arr[i];
arr[i] = arr[j];
arr[j] = tmp;
}
public void bubbleSort(int[] arr) {
for (int i = 0; i < arr.length - 1; ++i) {
for (int j = 0; j < arr.length - 1; ++j) {
if (arr[j] > arr[j + 1]) {
swap(arr, j, j + 1);
}
}
}
}
하지만 예를 들어 [1, 2, 3, 4, 5, 6] 같은 경우 swap 을 하지 않기 때문에 계속 bubble sort 한다는것은 낭비입니다. 또한 [2, 3, 1, 4, 5, 6] 같은 경우에 bubble sort loop 이 한 번 돌아가면 [2, 1, 3, 4, 5, 6] 이 됩니다. 3 4 5 6 은 어차피 정렬이 되어있는데 bubble sort을 할 필요가 있을까요? 따라서 조금 더 optimized 할 수 있어 보입니다.
public void bubleSortOpt(int[] arr) {
int lastSwappedIndex = arr.length - 1;
for (int i = 0; i < arr.length - 1; ++i) {
boolean isSwapped = false;
int lastSwapIndTmp = 0;
for (int j = 0; j < lastSwappedIndex; ++j) {
if (arr[j] > arr[j + 1]) {
swap(arr, j, j + 1);
lastSwapIndTmp = j;
isSwapped = true;
}
}
lastSwappedIndex = lastSwapIndTmp;
if (!isSwapped) break;
}
}
정렬 특성을 생각해보면 [1, 2, 3, 4, 5, 6] 같은 경우 loop 을 한 번 만 돌아도 더 이상 swap 을 하지 않았기 때문에 종료됩니다. O(n) 이 특성은 Adaptive죠.
Memory는 배열의 길이에 따라 바뀌지 않기 때문에 in-place
같은 수의 경우 swap 이 안되기 때문에 순서가 유지 됩니다. Stable
이 정렬 특성들이 궁금하다면 특성
Bubble Sort 특성
| Stability | Adaptivity | In-Place |
|---|---|---|
| Y | Y | Y |
Bubble Sort Big O
| Best | Avg | Worst |
|---|---|---|
| $$O(n)$$ | $$O(n^2)$$ | $$O(n^2)$$ |
'알고리즘 > 정렬' 카테고리의 다른 글
| Sorting Basic (0) | 2018.09.22 |
|---|
Comments
